
当研究室は、純粋な有機物から遷移金属錯体まで多岐にわたる「分子」を構成成分とする、機能性物質、特に超伝導体を含む電気伝導体の開発を行っている。分子性導体は、みかけの複雑さに反して、明快で見通しの良い電子構造を持つ。その多様な物性は、低次元性、強い電子相関、格子の柔らかさなどに由来している。分子性導体では、多様な分子修飾が可能であり、分子修飾による物性の精緻な制御が可能である。我々は、分子集合体の物性を合成化学的手法で制御することによって新しい物質を創造し、分子の特性を反映した新しい機能や現象を見いだすことを目指している。
- 三角格子を形成する分子性導体(Cation+)[Pd(dmit)2]2の反強磁性秩序構造(上田、藤山、崔、加藤;山本(浩))
- 反強磁性-量子スピン液体量子相転移近傍に位置するMe4Sb[Pd(dmit)2]2の磁性(藤山、上田、加藤)
- β'-X[Pd(dmit)2]2における圧力下ホール効果測定(岩瀬、上田、崔、加藤;山本(浩))
- 単一成分分子性超伝導体の発見(崔、岩瀬、加藤;小林(速)、石橋、佐々、小林(昭))
- 高圧下における単一成分分子性結晶のディラック・コーンの生成(圓谷、崔、加藤;木野、宮崎)
- Bi-layer系分子性導体(Me-3,5-DIP)[Ni(dmit)2]2の電子スピン共鳴およびサイクロトロン共鳴(大島、崔、加藤;高坂、売市、山本(浩))
- 電気二重層トランジスタを用いた有機モット絶縁体に対する高密度キャリアドーピング(川椙、佐藤、加藤;枝川、蒲江、竹延、山本(浩))
- 有機モットFETにおける金属絶縁体転移の臨界挙動(佐藤、川椙、加藤;須田、山本(浩))
- 三角格子を形成する分子性導体(Cation+)[Pd(dmit)2]2の反強磁性秩序構造
- 反強磁性-量子スピン液体量子相転移近傍に位置するMe4Sb[Pd(dmit)2]2の磁性
- β'-X[Pd(dmit)2]2における圧力下ホール効果測定
- 単一成分分子性超伝導体の発見
- 高圧下における単一成分分子性結晶のディラック・コーンの生成
- Bi-layer系分子性導体(Me-3,5-DIP)[Ni(dmit)2]2の電子スピン共鳴およびサイクロトロン共鳴
- 電気二重層トランジスタを用いた有機モット絶縁体に対する高密度キャリアドーピング
- 有機モットFETにおける金属絶縁体転移の臨界挙動
研究担当者:上田、藤山、崔、加藤;山本(浩)
分子性導体EtMe3Sb[Pd(dmit)2]2は、二次元三角格子上に局在するスピンの量子スピン液体(QSL)状態が実現すると考えられており、実験、理論的研究が盛んにおこなわれている。EtMe3Sb塩を含む、(Cation+)[Pd(dmit)2]2の多くは、同形構造をとる。二量体[Pd(dmit)2]2− 間の移動積分が、対カチオンに応じて異なる異方性パラメーター(t'/t; t, t'は移動積分)で特徴づけられる二次元の二等辺三角形格子スピン系を形成する。QSLは、t'/tが1に近い塩で現れ、t'/tが小さい塩では、反強磁性秩序(AFLO)が発現する1。QSLに隣接するAFLOがどのような、秩序構造を持つのかを明らかにすること、フラストレーションスピン系の理解のために重要である。そこで、AFLOおよびQSLを発現する各種カチオン塩の磁気異方性(二次元面に垂直/平行方向)を、MPMSを用いて2Kまで測定することで、磁気秩序構造とフラストレーションとの相関について調べた。
QSLを発現するEtMe3Sb塩は、二次元面に垂直/平行方向の磁化率が等しく、磁気異方性を示さず、異方的な磁気秩序の発達が無いことが確認された。このことは、磁気トルクの実験とコンシステントである。AFLOを発現すると理解されているほとんどの塩(Me4P塩〜Et2Me2As塩;0.62 ≤ t'/t ≤ 0.87)では反強磁性秩序温度(TN)以下で、二次元面に垂直方向と平行方向の磁化率が分裂し、磁化容易軸は二次元面に垂直であると決定された。ところが、t'/t-T相図上でQSLに隣接し、最も低いTN(16 K)を与える、Me4Sb塩では、基底状態は反強磁性秩序状態にあるとされているにもかかわらず、QSLを発現するEtMe3Sb塩同様に、磁気異方性が観察されなかった。Me4Sb塩の特異性は、M-H曲線においても観察され、他のAFLO塩ではスピンフロップ転移様の磁気異常が観測されるのに対して、Me4Sb塩とEtMe3Sb塩は、7Tまで磁気異常が見られなかった。近年、我々の研究室では、カチオン層を混晶化することで、t'/tを精密調整することに成功している2。典型的AFLOを示す、Et2Me2As塩にEt2Me2Sb+を加えていくと、t'/tの変化にともなって、基底状態がAFLOからQSLへと変化することを昨年までに報告している。そこで、Et2Me2As1-xSbx[Pd(dmit)2]2カチオン混晶塩をもちいて、Me4Sb塩の特異性が、Me4Sb塩に特有なものなのか、それとも、t'/tに依存して現れるものなのかを検討した。0 ≤ x ≤ 0.05塩は、磁気異方性、スピンフロップ転移ともに観測され典型的AFLOとして振る舞い、0.35 ≤ x塩では、QSLとして振る舞ったのに対して、それらの中間の0.15 ≤ x ≤ 0.25では、Me4Sbと同様の磁気的振舞いが観測された。(Cation+)[Pd(dmit)2]2では、三角格子のフラストレーションに由来して、AFLOとQSLの境界付近に、AFLOとQSLの中間的な特異な磁気状態が実現すると結論付けられた。この磁気状態がどのような秩序状態にあるのか、または、揺らぎに支配された状態なのかは未解明である。そのミクロな磁気構造を明らかにするために、現在Me4Sb塩の13C NMR測定にとりかかったところにある。
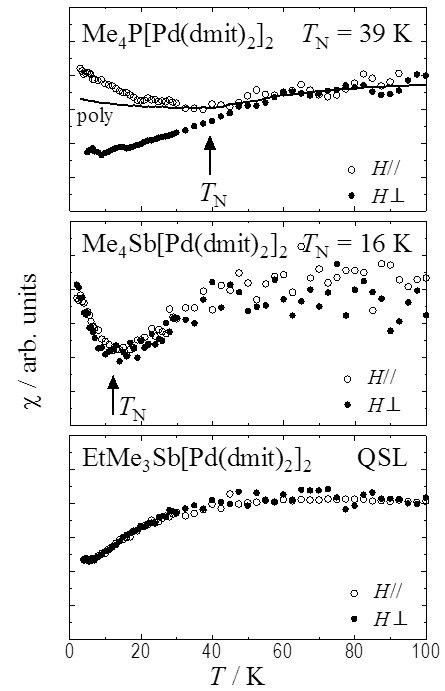
Magnetic susceptibility of (Cation+)[Pd(dmit)2]2
【参考文献】
[1] K. Kanoda and R. Kato, Annu. Rev. Condens. Matter Phys., 2, 167-188 (2011).
[2] R. Kato et al., Phys. Status Solidi B249(5), 999-1003 (2012).
研究担当者:藤山、上田、加藤
β'-Pd(dmit)2系のt'/t-T相図中で反強磁性秩序と量子スピン液体相の臨界領域に位置すると考えられているMe4Sb[Pd(dmit)2]2は磁化測定からT~10Kという低温で長距離秩序の存在が示唆されるものの、磁気相転移温度以下で磁気異方性が観測されない。これは高い反強磁性転移温度を示す、t'/tが小さい領域に位置する試料の反強磁性秩序状態とは対照的な振る舞いであり、隣接する量子スピン液体相との関連などに興味が持たれる。
粉末試料を用いた13C NMRスペクトルは10K以下で顕著な線幅の増大を示し、秩序モーメントの出現を示す。一方、磁気秩序温度以下のスペクトルは共線的な反強磁性秩序状態で期待される、信号強度が周波数にほとんど依存しないスペクトルとは大きく異なり、中心周波数付近に構造を持つ。これは、電子密度の大きく異なる二種以上の13Cサイトの存在を示す。これまでβ'-Pd(dmit)2系においては、他の分子性導体で観測されるような電子間クーロン反発に起源を持つ電荷秩序の可能性は指摘されておらず、NMRスペクトルから示唆される不均一な電子密度分布はPd(dmit)2分子内の自由度に起因した現象である可能性を指摘できる。

磁気秩序を示すMe4Sb[Pd(dmit)2]2の13C NMRスペクトル。
10K以下でスペクトル線幅の顕著な増大を示すが、中心周波数付近に鋭い構造を持つ。
研究担当者:岩瀬、上田、崔、加藤;山本(浩)
金属錯体β'-X[Pd(dmit)2]2は、カチオンXの違いにともなう結晶構造のわずかな相違により電子相関に基づく多彩な電子状態を示す。電子状態を理解するための基本的なパラメータとして、[Pd(dmit)2]2-二量体を1つのユニットとみなした時の三角格子の異方性パラメータt'/t (t', tはダイマー間の移動積分)をあげることができる。t'/tが1より十分小さい場合には、基底状態は反強磁性相、1より大きい場合には電荷秩序である。一方、t'/tが1に近い場合、つまり正三角格子を組む場合であるが、この場合スピンの秩序化が低温まで起こらない量子スピン液体状態が観測されている。
今年度の研究目的は、常圧下で反強磁性を示すβ'-Et2Me2As[Pd(dmit)2]2におけるホール効果測定を行うことで電子物性の新しい側面を見いだすことであった。この物質は、約16 Kで反強磁性転移し、圧力下で超伝導転移することがわかっている。今年度のはじめにホール効果測定用のプローブを製作した。このプローブには、磁場反転を行うために回転機構を取り付けてある。回転はプローブの上部に取り付けたステッピングモーター(400ステップ)で駆動し、1/128マイクロステッピングドライバおよび歯車(歯車比1:6)により~0.001°の高い回転精度を持たせた。
単結晶試料β'-Et2Me2As[Pd(dmit)2]2およびβ'-Et2Me2As0.5Sb0.5[Pd(dmit)2]2に対し、5または6端子法により試料回転および磁場スイープ両方の測定方法を使ってホール係数および電気抵抗の温度依存性を調べた。その結果明らかになったことを以下に示す。
1.200 Kではホール係数RHが正の値(~10-2 (cm3C-1))であり、ホール伝導が主体である。RHは温度を下げるにしたがって上昇するが圧力によって上昇は抑えられていく。RHの符号が反転するものもあったが再現はできていない。
2.磁気抵抗Rxxの磁場依存性は、約30 K以下で正から負へ変化する。
3.β'-Et2Me2As[Pd(dmit)2]2に関して、電気抵抗が急激に減少してしまう問題が起きやすい。10個以上の試料依存性を測定する必要があった。超伝導転移は明確に確認することができる。
4.AsとSbの混晶系において、Asの混晶比が増加するにしたがって超伝導の転移圧力が上昇していく傾向がある。
5.圧力下低温(例えば8 kbar・20 K近傍)で、電気抵抗の異常が必ず観測される。それ以上の圧力をかけると異常温度が上昇するとともに弱くなり、わずかな折れ曲がりだけとなる。このような振る舞いがホール係数と関連しているのではないかと推測しているが、多数の試料に対して測定し再現性を調べる必要がある。反強磁性転移に伴う磁気的なものがトランスポートに反映しているのかどうかも興味深い点である。
このようにホール効果および電気抵抗についてこれまで知られていなかった振る舞いが明らかになってきた。今後、より信頼性の高いデータを取得する必要がある。
研究担当者:崔、岩瀬、加藤;小林(速)、石橋、佐々、小林(昭)
2001年に、初めての単一成分分子性金属である[Ni(tmdt)2]が発見されて以来[1]、単一成分からなる分子性金属および超伝導体の探索が盛んに行われるようになった。従来の分子性伝導体は、二種類以上の成分から構成されるが、単一成分分子性導体は一種類の分子だけで構成されている特徴を持っている。しかし、伝導性の良い単結晶の作製が非常に難しく、常圧で低温まで金属性を示す単一成分分子性導体は [M(tmdt)2]系以外発見されていない。一方、伝導性の悪い単一成分分子性結晶は比較的大きな結晶を得易い。そのため、絶縁性結晶への超高圧印加は、単一成分分子性金属の探索において非常に有効な手段である。私達は最近、ダイヤモンドアンビルセル(DAC)を用いた四端子法により、常圧では絶縁体である単一成分分子性導体[Ni(ptdt)2]単結晶が19 GPaで金属になることを発見した[2]。更に、小さいリガンドを持つ単一成分分子性半導体[Ni(dmit)2]単結晶が約16 GPaで金属状態が現れ、25.5GPaまでその金属状態が維持されることを発見した[3]。しかし、今までの研究では超伝導体の発見に至っていない。今回、常圧で絶縁体である、単一成分分子性単結晶Ni(hfdt)2]の高圧下電気伝導度を測定した結果、単一成分分子性導体では最初の超伝導体を発見した[4]。

図1:分子構造
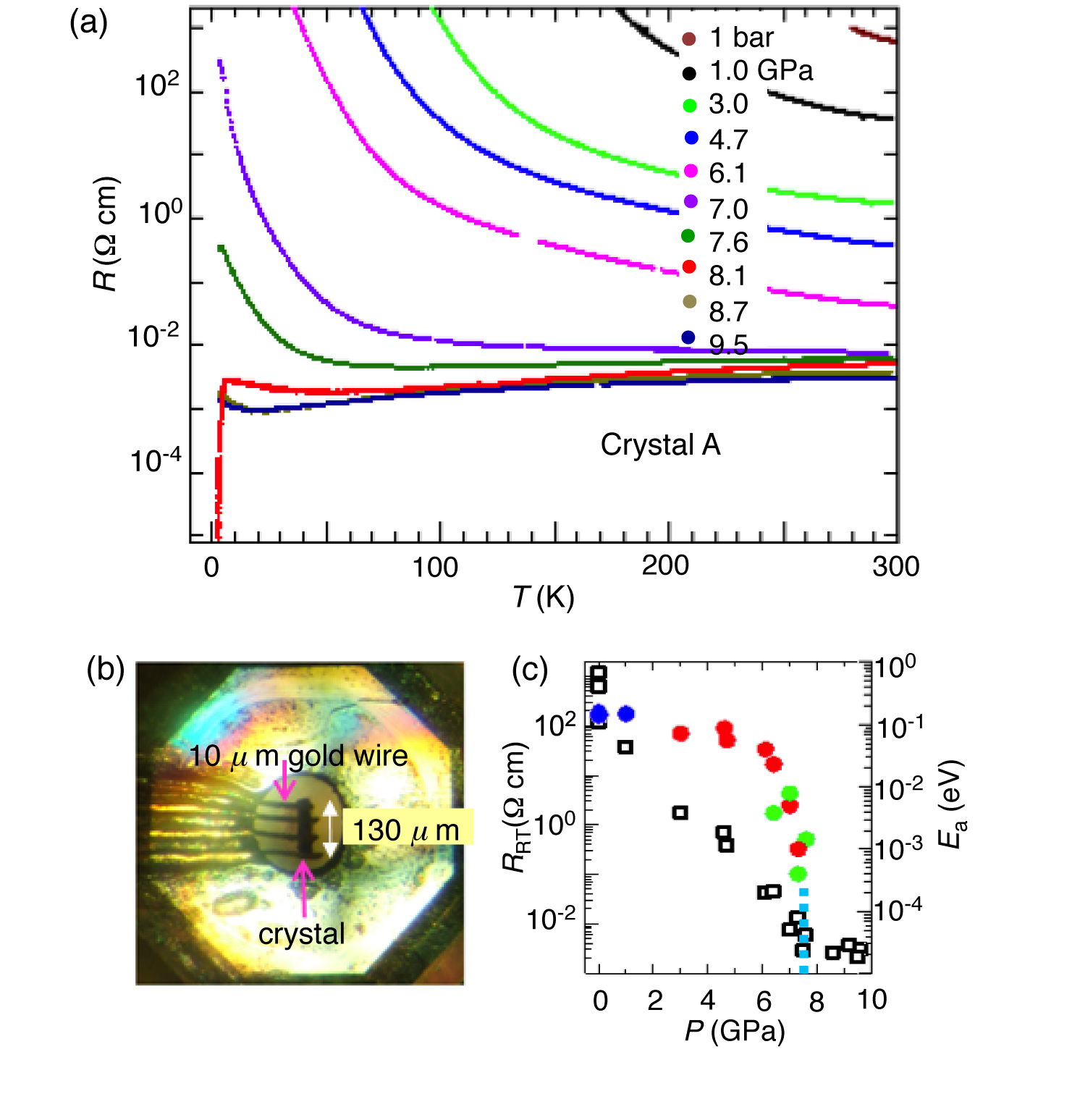
図2:(a)抵抗率の温度依存性 (b)サンプルの圧力下写真 (c)室温抵抗率と活性化エネルギーの圧力依存性
[Ni(hfdt)2]単結晶は電解酸化法で作製した。室温電気抵抗率は約6 × 102 Ω cmであり、活性化エネルギー(Ea) は0.14 eVである。直径0.7mmのDACを用いて、ガスケットはステンレス鋼SUS 301を使用し、圧力媒体はDaphne oil 7373を使用した。試料に10 mの金線と金ペイントで配線し、電気抵抗測定は直流四端子法で行った。圧力はルビー蛍光測定装置を用いて室温でR1ラインのシフトを測定することにより決定した。図2に示したように、室温電気抵抗率は圧力印加とともに急激に減少し、7.3 GPaでは約3 × 10-3 Ω cm になる。一方、活性化エネルギーは6 GPaまでゆっくり減少するが、それ以上の圧力で急激に減少し、7.5GPaでは金属状態が現れる。7.6 GPaでの電気抵抗率の温度依存性測定では、室温から85 Kまで金属状態を保ち、それ以下の温度では電気抵抗率はゆっくり上昇するが、約5 K付近でわずかに減少する。更に高い圧力では、転移温度が少し上昇しながら、電気抵抗率の減少が鋭くなる。8.1 GPaでは転移温度が5.5 Kであり、外部磁場を印加しながら電気抵抗率の測定を行った結果を図3に示した。電気抵抗率の転移温度は磁場が強くなるとともに低い温度へシフトし、この転移が超伝導転移であることが証明された。この超伝導転移温度は8.1GPaで最大値をとり、更に高い圧力では少し低温側にシフトする。8.7 GPaでは完全に消失し、それ以上の圧力では超伝導状態が確認されていない。この測定結果から得られた圧力-温度相図を図3cに示した。圧力下での電気的性質をよく理解するため、第一原理手法を用いた圧力下でのバンド構造計算を6~11GPa領域で計算を行い、その結果を図4に示した。計算から得られた常圧での活性化エネルギーは0.12 eVであり、6 GPaで0.01 eVに減少する。8 GPaではバンドギャップが完全に消失するともとに電子とホールの小さいポケットに由来する三次元的フェルミ面が現れる。更に高い圧力を印加するとフェルミ面が大きく成長し、二次元的フェルミ面が得られ、実験結果から得られた圧力下での金属化現象を良く説明できる。
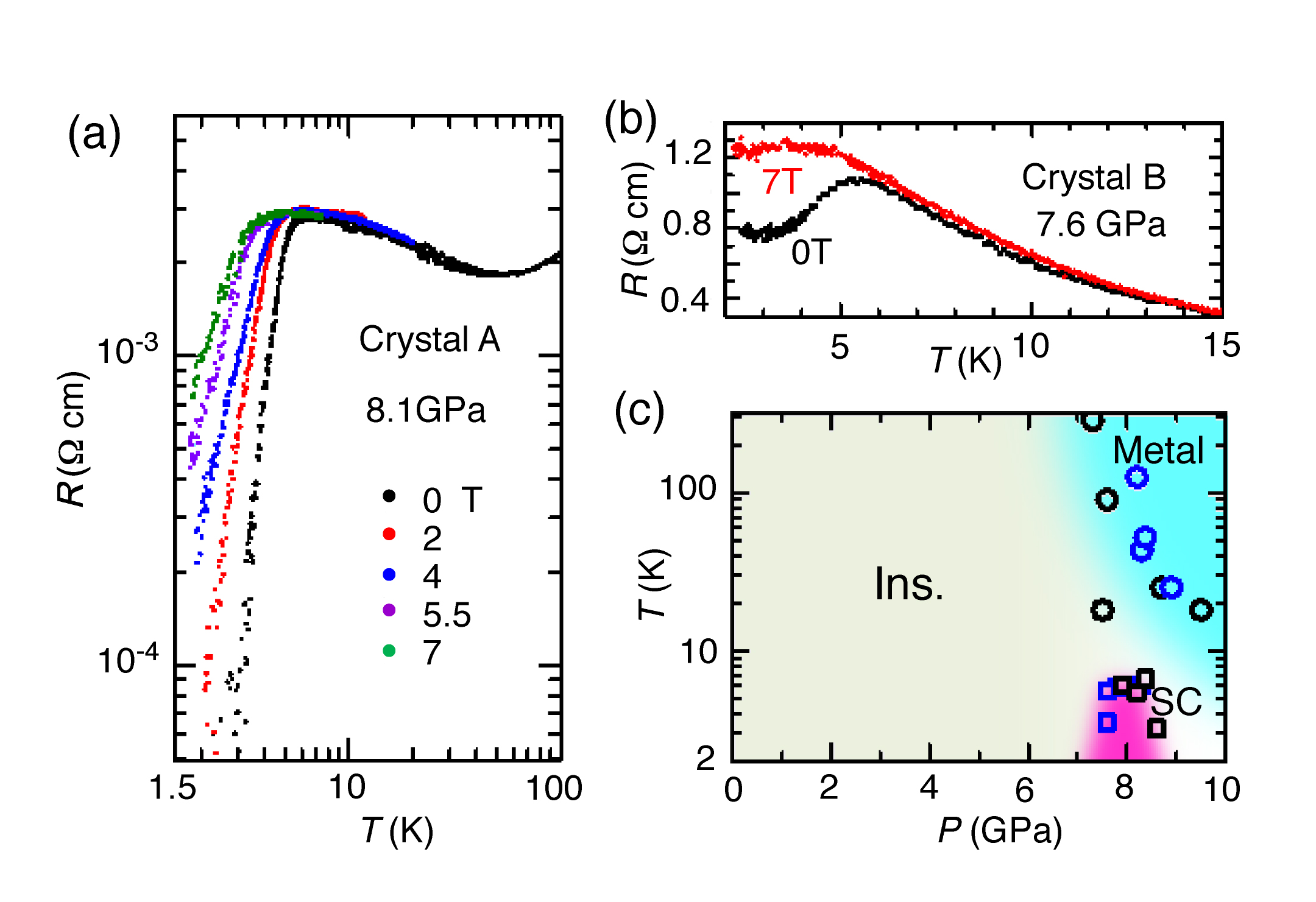
図3:電気抵抗率の磁場依存性。(a)8.1GPa (b)7.8GPa (c)圧力-温度相図

図4:(a) 8 GPa下での分散曲線 (b) 8 GPa下電子状態密度 (c) 8GPa、10 GPaでのフェルミ面
【参考文献】
[1] Tanaka, H.; Okano, Y.; Kobayashi, H.; Suzuki, W.; Kobayashi, A. Science 2001, 291, 285
[2] Cui, H. B.; Brooks, J. S.; Kobayashi, A.; Kobayashi, H. J. Am. Chem. Soc. 2009, 131, 6358
[3] Cui, H. B.; Tsumuraya, T.; Miyazaki, T.; Y. Okano, Y.; Kato, R. Eur. J. Inorg. Chem. 2014, 24, 3837
[4] Cui H. B.; Kobayashi H.; Ishibashi S.; Sasa M.; Iwase F.; Kato R.; and Kobayashi A. J. Am. Chem. Soc. 2014, 136, 7619
研究担当者:圓谷、崔、加藤;木野、宮崎
ディラックコーンとは、フェルミ準位近傍の特異点のみで接する線形なエネルギー分散を持つ特異な電子構造である。このような電子構造では、有効質量を定義できないため、高いキャリア速度を示すため、注目を集めている。これまで、グラフェン、トポロジカル絶縁体の表面状態、分子性導体(圧力下のα-(BEDT-TTF)I3)といった物質においてディラックコーンが確認されている。
単一中性分子で構成されている分子性結晶の多くは、常圧で半導体的な性質を示す。その中でも金属ジチオレン錯体は、分子のHOMO-LUMO準位差が比較的小さく(計算値 ~0.6 eV)、共役が空間的に広がっている。このことにより、HOMO由来のバンドとLUMO由来のバンドの重なりによる金属化が容易に起こることが期待される。実際、Ni(tmdt)2 (tmdt = trimethylenetetrathia fulvalenedithiolate)のように分子が比較的大きい場合には、常圧においても金属状態が実現されている [1] 。一方、Ni(dmit)2(dmit = 1,3-dithiole-2-thione-4,5-dithiolate)のように分子が小さく、常圧で半導体的な性質を示す単一成分系であっても、最近、ダイアモンドアンビルセル(DAC)を用いて25 GPa 以上の圧力下まで4端子法による電気抵抗測定を行うことが可能となり、いくつかの単一成分分子結晶において8 GPa以上で金属化[2]、または超伝導状態[3]を実現することを報告している。しかし、このような物質の圧力下の構造と電子状態を実験のみから決定することは難しく、実験結果に依存せずにそれらを決定できる第一原理計算手法は、物性とその機構を理解する上で大変有効なアプローチとなっている。
今回、多種多様な単一成分分子性結晶の静水圧下における構造と電子状態を密度汎関数理論に基づく第一原理計算手法を用いて調べた結果、Pd(dddt)2 (dddt = 5,6-dihydro-1,4-dithiin- 2,3-dithiolate)が8 GPa程度の圧力下でフェルミ準位に線形なバンド分散(ディラックコーン)を持つことがわかった。また、最近測定された電気抵抗は、11.6 GPaで室温における電気抵抗は1Ωcmまで低下し、半金属的な性質を示している。12.6 GPaにおける温度依存性は、ほぼ温度に依存せず水平となる結果を得ている。これは、グラフェンやα-(BEDT-TTF)I3といったディラック電子系に共通した特徴的な振る舞いである[4]。
図1に常圧におけるPd(dddt)2の結晶構造(単斜晶系; 空間群 P21/c)を示す。結晶格子のb軸方向にPd(dddt)2分子が積層していることに対応して、Г&GammaY方向に一次元的なバンド分散を持つことがわかった。単位胞に結晶学的に独立な2種類の分子が2つずつ存在していることから、フェルミ準位近傍にはHOMO由来のバンドとLUMO由来のバンドが4本ずつ現れる。(図2(a)) 加圧とともにバンド幅は広がっていき、HOMOバンドとLUMOバンドは8 GPaにおいて点で接することがわかった。(図2(b))ディラック点は、a-c面内と図2(c)に示すようなb*軸上(kx, kz = 0)に存在しており、その周りで線形なバンド分散をもち、バンドギャップはゼロとなっている。
ディラックコーンの生成機構を明らかにするために、電子状態を解析した。常圧において、価電子帯は、Pd(dddt)2孤立分子のHOMO軌道と同様の波動関数で構成されている。8GPaになると、このHOMOバンドに対してオフサイトの分子のLUMO軌道などと混成が強められていることがわかり、この多軌道性がディラックコーンの生成に、大きな役割を果たしていると考えられる。さらに加圧によって、系の次元性がどのように変化したのかを理解するために、フェルミ準位の上下の低エネルギーレベルにおいて、仮想的なフェルミ面を計算した結果、a*+c*とb*方向で擬二次元面を作っていることがわかった。これらの結果は、加圧によって分子間距離が短くなった結果、分子間の異なる軌道との混成が強まり、さらに、常圧で一次元的であった系が擬二次元的へと変化したことを示している。
第一原理計算により決定した8 GPaでの結晶構造を用いて、拡張ヒュッケル法に基づくtight-binding計算をHOMOとLUMOの重なり積分を考慮して実行した結果、概ね第一原理計算のバンド構造を再現することができた。常圧からHOMO-LUMOの重なり積分は無視できず、8 GPaにおいて、特に分子の積層方向であるb方向とa+c方向の重なり積分が顕著に増大する。また、積層方向の重なり積分が逆符号になっているために、HOMOバンドがすべて上に凸になっているのに対して、LUMOバンド(の一つ)が下に凸になっていることが、ディラックコーンの生成に重要であると考えられる。
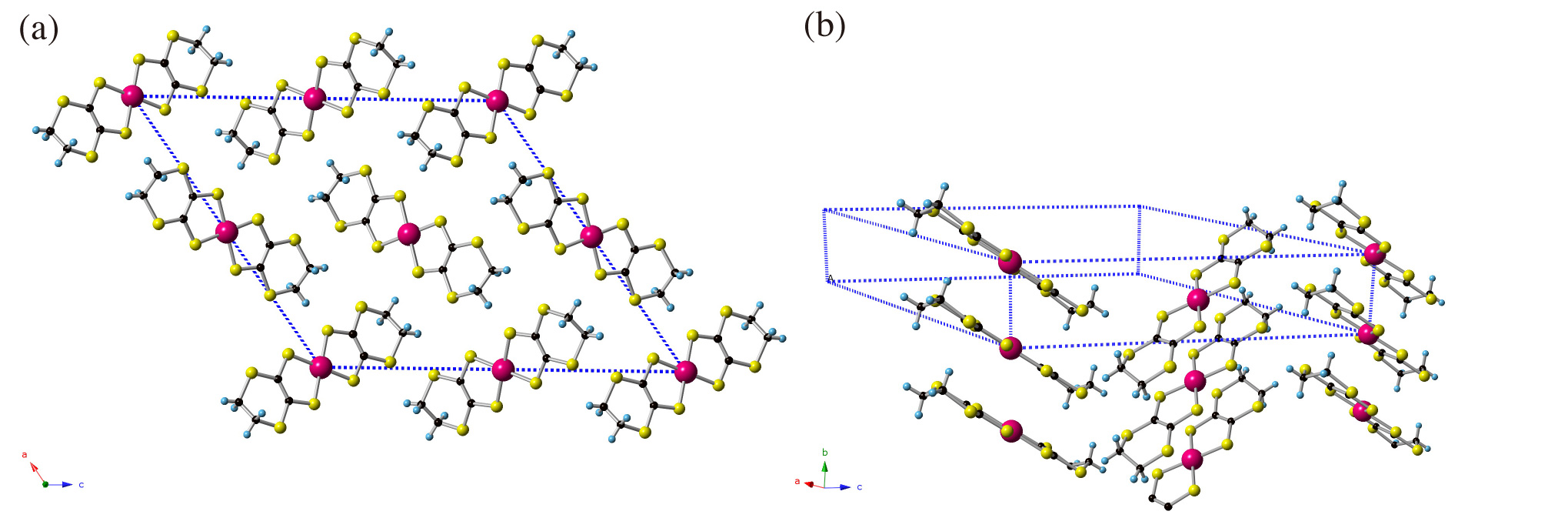
図1:常圧における結晶構造。(a) a-c面、(b) b-c面

図2:(a) 常圧、(b) 8 GPaにおけるバンド構造、(c)三次元バンド構造
[1] H. Tanaka, Y. Okano, H. Kobayashi, W. Suzuki, A. Kobayashi, Science, 291, 285 (2001).
[2] H. B. Cui, T. Tsumuraya, T. Miyazaki, Y. Okano, and R. Kato, Eur. J. Inorg. Chem, 24, 3837 (2014).
[3] H. B. Cui, H. Kobayashi, S. Ishibashi, M. Sasa, F. Iwase, R. Kato, and A. Kobayashi, J. Am. Chem. Soc., 136, 7619 (2014).
[4] N. Tajima, S. Sugawara , M. Tamura, Y. Nishio, and K. Kajita, J. Phys. Soc. Jpn. 75, 051010 (2006).
研究担当者:大島、崔、加藤;高坂、売市、山本(浩)
局在電子と遍歴電子が相互作用する系は、巨大磁気抵抗効果や磁場誘起超伝導など、興味深い物性を示す事からこれまで多くの注目を集めてきた。特に、局在d電子と遍歴π電子が相互作用するλ-(BETS)2FeCl4 (BETS = bis(ethylenedithio)tetraselenafulvalene) ではFe3+(S=5/2)の3d電子の反強磁性秩序化に伴いπ電子は金属-絶縁体転移を起こすが、これに磁場を印加し3d電子スピンを偏極させるとπ電子が金属化し、さらに磁場を加えると約17 Tで超伝導状態となる[1]。このように局在電子と遍歴電子が相互作用する系は多彩な電子状態を示す。
我々の研究室では、分子性物質の設計性や分子配列の自由度を活かした、Bi-layer系物質が多く開発されており[2-4]、その一つが図1の(Me-3,5-DIP)[Ni(dmit)2]2 (Me=methyl, DIP=diiodopyridinium, dmit=1,3-dithiole-2-thione-4,5- dithiolate)である。この物質は Me-3,5-DIPカチオンの影響を受けて、2つの異なるNi(dmit)2層が形成され、Layer IではNi(dmit)2分子が強く二量体化し、Layer IIではNi(dmit)2分子同士がまたがるような構造をとる(図1)。バンド計算から、Layer IがMott絶縁層、Layer IIが二次元的な伝導層となることが予想され、NMRや磁気抵抗・量子振動の測定からも、それらを示唆する結果が得られている [5,6]。また量子振動の測定から、Layer I(絶縁層)からの内部磁場によりLayer II(金属層)のフェルミ面が分裂しているのが観測されており、局在電子と遍歴電子の強い相互作用が示唆されている[6]。一方で、局在π電子からなるLayer Iの磁性は未解明のままであり、NMR測定から約2 Kで反強磁性転移もしくはスピン相関の強い揺らぎが示唆されているが[5]、熱容量測定から相転移は観測されていない。そこで、我々はミクロな電子状態の最も直接的なプローブ法である、電子スピン共鳴(ESR)とサイクロトロン共鳴(CR)に着目した。(Me-3,5-DIP)[Ni(dmit)2]2のLayer I(絶縁層)でESRを観測し、Layer II(金属層)でCRを観測すれば、異なる物性を持つ層を区別して各々の電子状態をミクロに知ることが可能である。
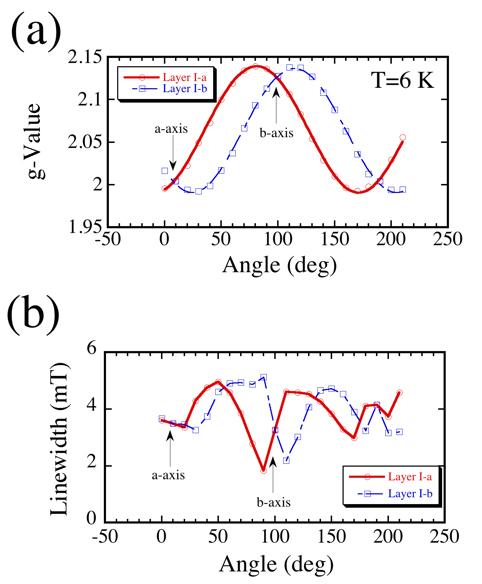
(Me-3,5-DIP)[Ni(dmit)2]2において磁場をab面内に回転させた時のESR測定から得られた、g値の面内角度依存性を図2(a)に示す。Ni(dmit)2分子のd軌道の混成を反映して、g値は大きな異方性を示す。また、磁場の方位によってESR信号が2つに分裂している。g値の主軸は[Ni(dmit)2]2ダイマーのスタック方向とその垂直方向に対応しており、2つのESR信号はダイマーのスタック方向が異なるLayer I-aとI-bに各々相当する。また、2つの絶縁層のESR信号が独立して観測されていることから、Layer I-aとI-bには相互作用がない事もわかる。一方でESR線幅の角度依存性(図2(b))も興味深い。Layer I-aとI-bともに似たような振る舞いを示すが、どちらともb軸近傍で急激な線幅の先鋭化が見られ、通常の磁性体とは異なる線幅の振る舞いを示す。奇しくもB//b軸方向はトンネリングの運動量シフトによる異常な磁気抵抗が観測されており[6]、この急激な線幅の先鋭化はLayer IIの伝導π電子との相関によるものであると考えられる。この事と絶縁層Layer I-aとI-b間に相互作用がないのは一見矛盾しているように見えるが、自由な伝導π電子からなるLayer II(金属層)がLayer Iの局在スピンの層間方向への長距離秩序化を阻害していると考えれば説明がつく。実際、約1.6 Kまで反強磁性共鳴は観測されておらず、長距離秩序化は起こっていないと考えられる。この結果は磁気トルク測定の結果とコンシステントである[6]。
図3は(Me-3,5-DIP)[Ni(dmit)2]2のCR測定の結果である。磁場はB//c*軸に印加しており、線幅の狭いESR(この磁場方向では1つの信号に見える)の他にLayer II由来で広い線幅のCRが観測されている。共鳴磁場から導出される有効質量は約m*=0.94meである。この結果は量子振動の結果m*=6meと大きくかけ離れており、Kohnの定理より、Layer IからLayer IIへの相互作用の寄与が非常に大きいと結論付けられる。
 |
 |
|
| 図1:(Me-3,5-DIP)[Ni(dmit)2]2の結晶構造。 Layer I-aとI-bではダイマーのスタック方向が僅かに異なる。 |
図2: ESR信号より得られた (a) g値と (b) 線幅のab面内における角度依存性。 2つのESR信号が観測されており、各々Layer I-aとI-bに相当。 |

図3:B//c*におけるミリ波測定の結果。
ESRと線幅がブロードなCRが観測されている。
【参考文献】
[1] S. Uji et al., J. Phys. Soc. Jpn. 75, 051014 (2006).
[2] Y. Kosaka et al., J. Am. Chem. Soc. 129, 3054 (2007)
[3] T. Kusamoto et al., Inorg. Chem. 51, 11645 (2012).
[4] T. Kusamoto et al., Inorg. Chem. 52, 4759 (2013).
[5] S. Fujiyama et al. Phys. Rev. B 77, 060403(R) [6] K. Hazama et al. Phys. Rev. B 83, 165129 (2011).
研究担当者:川椙、佐藤、加藤;枝川、蒲江、竹延、山本(浩)
ある固体が金属か、絶縁体かといった基本的な電子状態は、一体近似のバンド理論によって説明することができる。ところがモット絶縁体と呼ばれる物質群は、バンド理論では金属であると予測されるにもかかわらず、強い電子間反発のために絶縁体になっている。いわゆる高温超伝導体の母体物質がモット絶縁体であることから、モット絶縁相とその近傍の電子状態は、物性物理学の主要な研究対象のひとつで有り続けている。
モット絶縁体を金属や超伝導体にするには二つの方法が知られている。ひとつは高温超伝導体で行われているように、電子や正孔といった電荷担体(キャリア)をドープする方法で、もうひとつが圧力をかけて格子を縮め、電子を動きやすくする方法である。有機モット絶縁体ではその柔らかさを活かして、伝統的に後者の方法が用いられてきたが、最近、加藤Gによって電界効果トランジスタ(FET)の構造を用いたキャリアドーピングが可能であることが明らかになった[1]。これによって両方の手法を同じ物質に適用することが可能になり、電子間反発の強い系における物理の、ひいては超伝導現象の起源の解明につながると期待される。しかしながら、FETではゲート絶縁膜の耐電圧を超えると絶縁破壊が起こるため、最大でも元のキャリア数の10%程度しかドープできなかった。そこで、最近新たなキャリアドーピングの手法として注目されている電気二重層トランジスタ(EDLT)の構造を有機モット絶縁体に適用し、高密度のキャリアドーピングを試みた。
有機モット絶縁体κ-(BEDT-TTF)2Cu[N(CN)2]Cl (略称:κ-Cl)の薄片状の単結晶を用いてFETとEDLTを作製し、それぞれの電界効果を比較すると(図1)、EDLTではFETの少なくとも4倍以上のキャリアをドープできることがわかった。これによって、電子ドープした試料は金属化、正孔ドープ側でも数桁以上抵抗が減少し、同一試料の電子ドープした状態、正孔ドープした状態でそれぞれホール効果を測定することが可能になった。
ホール係数から見積ったキャリア数は、一般的なトランジスタではゲート電圧に比例して増加する。ところがこの試料では、図2(a)に示すように、キャリア数はサンプルやゲート電圧によらず、ほぼ一定の値を示す。この値は電子ドープ状態で約4 /Tであり、電子間反発がなければ動けるはずのキャリアの80~90%程度がキャリアドーピングによって動けるようになったことを示唆している。言い換えれば、電子間反発によって固体化していた電子がキャリアドーピングによって融解するというモット絶縁体に特有の著しい特徴をとらえている。
この特徴は、正孔をドープした時も同様に観測されると期待される。実際に正孔ドープ状態でもサンプルやゲート電圧によらずホール係数はほぼ一定の値を示した。しかし、驚いたことにその値は電子ドープ側と比べ3倍程度も大きく、電子状態がモット絶縁相を挟んで明確に異なることがわかった(図2(b),(c))。この大きなホール係数(少ないキャリア数)の原因は明らかでないが、κ-BEDT-TTF塩で理論的に予言されている擬ギャップ状態[2]を仮定すると矛盾なく説明される。つまり、電子ドープ側は反強磁性的なスピン相関が弱く、フェルミ液体状態に近い。一方で正孔ドープ側は反強磁性的なスピン相関が生き残り、擬ギャップ状態に対応していると考えることができる。このような磁性に関する電子-正孔非対称性は理論的にも予測されており[3]、異方的な格子を持つモット絶縁体に対するキャリアドーピングの本質をとらえている可能性を示唆している。高温超伝導の舞台である銅酸化物モット絶縁体では、酸素サイトへの電荷移動、軌道自由度、ドーパントによる乱れなど複雑な要因のためか見られなかった現象であり、シンプルな電子状態を持つモデル物質としての有機モット絶縁体の優位性を示す結果である。
(BEDT-TTF = bis(ethylenedithio)tetrathiafulvalene)
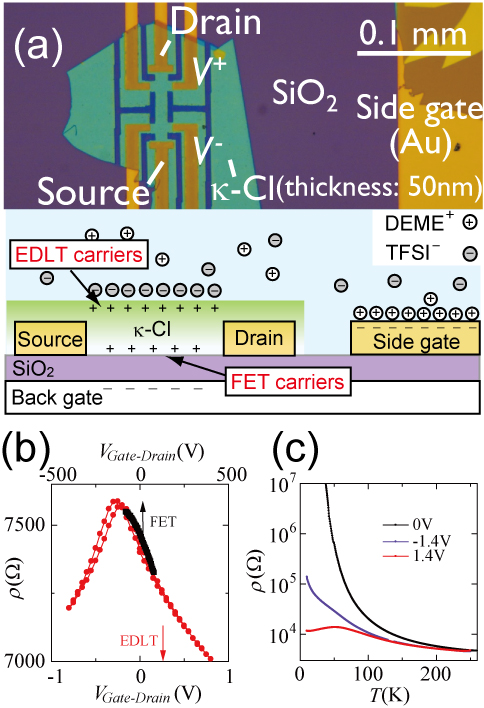
(b) 220Kにおける、EDLTとFETそれぞれの電界効果。
(c) EDLTでドープした試料の電気抵抗の温度依存性。+1.4Vは電子ドープに、-1.4Vは正孔ドープに対応する。
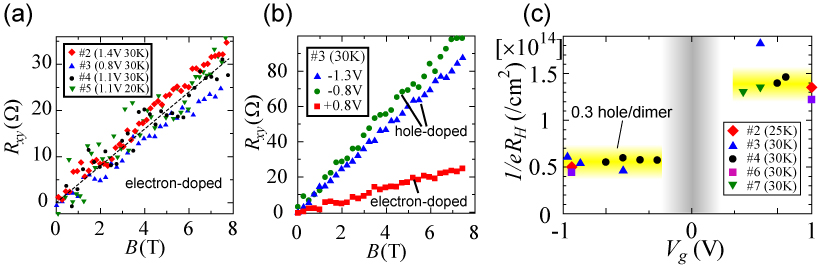
(a) 複数のサンプルにおける、電子ドープ状態のホール効果。傾きがホール係数を与える。
(b) 同一サンプルにおける電子ドーピング(正のゲート電圧)と正孔ドーピング(負のゲート電圧)の比較。
(c) ホール係数から見積ったキャリア数のゲート電圧依存性。
【参考文献】
[1] Kawasugi, Y.; Yamamoto, H. M.; Hosoda, M.; Tajima, N.; Fukunaga, T.; Tsukagoshi, K.; Kato, R. Appl. Phys. Lett. 2008, 92, 243508.
[2] Kang, J.; Yu, S.; Xiang, T.; Li, J. Phys. Rev. B 2011, 84, 064520.
[3] Kyung, B. Phys. Rev. B 2007, 75, 033102.
研究担当者:佐藤、川椙、加藤;須田、山本(浩)
分子性導体κ-(BEDT-TTF)2[Cu(CN)2]Cl (κ-Cl)は、低温では強い電子相関によりモット(Mott)絶縁体となる擬二次元強相関電子系である。これまでの研究で我々は、κ-Clやその姉妹物質であるκ-Brの薄片単結晶を用いた電界効果トランジスタ(モットFET)を作製し、電界効果を利用したキャリア注入を行うことで、分子性導体では従来困難だった電荷ドープによるフィリング制御型Mott相転移の実現に成功しており、その詳細について調べている。本手法は不純物の混入を伴わず、かつ精密にドーピング量を調節できるため、電子相関・乱れの効果が協同的に発現するとされる転移点近傍の物性を知る上で大変有用である。
FETでは原理上、その電子物性が基板/分子性導体チャネル界面の性質に鋭敏な影響を受けやすい。そこで我々は、アルキル基(C8H17-)末端またはパーフルオロアルキル基(C6F13C2H5-)末端を有する自己組織化単分子膜(Self-Assembled Monolayer; SAM)を利用した基板界面制御を行うとともに、分子層厚(1.5 nm)のレベルで平滑な表面有するκ-Cl薄膜単結晶(図1挿入図)の合成手法を見いだし、モットFETデバイス特性の性能(移動度、on/offスイッチング比)を向上させることに成功した。とりわけ20-40 Kの中低温領域に着目すると、ゲート電圧V_gの印加により金属-絶縁体(MI)転移が引き起こされることが明らかとなった(図2左)。転移点の電気伝導率はσ〜e2/h程度であるが(e:電荷素量、h:プランク定数)、これはGaAsなど高移動度低次元半導体系で見られるものと一致し、Mott-Ioffe-Regel限界を満たすものである。一方、ホール効果の測定から、本転移はキャリア密度一定(〜1014 cm-2)のもとで起こることが明らかとなっており、強相関系特有の性質を有していることがわかる。また、本MI転移の発現にはκ-Cl/基板の界面状態が強く影響することから、電子相関・構造乱れの双方が寄与するモット-アンダーソン(Anderson)転移の性質があることが示唆される。
図2右は、MI転移点近傍において様々なVg,Tにおける伝導度σに対し臨界スケーリングを行った結果を示したものである。量子相転移に関するスケーリング仮説によれば、MI転移近傍で相関長ξ、相関時間τがそれぞれξ∝|x-xc|-ν、τ∝|x-xc|-zνにしたがい発散する性質のため、臨界領域における伝導度はσ(T,x)=σc F(|x-xc| T-1/νz )という単一の関数で表すことができる(ν、zは転移のユニバーサリティークラスに依存する臨界指数、xはパラメーターでありここではゲート電圧に対応する)。実際、νz=1.6を仮定すると、20-30 Kで観測された全ての伝導度が転移点を挟んで金属側・絶縁体側に対応する2つの曲線上に乗り、本MI転移はスケーリング則に従っていることがわかる。さらに10 K以下の低温領域では、明確なMI転移が観測されなくなり、全ゲート電圧に対してΔσ〜(e2/h)logTTに従うような絶縁体的な電子輸送特性に移行する。しかしながら磁場に対する応答に着目すると、転移点を境に磁気抵抗の反転を伴うような大きな変化が依然として見られる。干渉効果が重要になる低温では、電子間反発による局在効果に加え弱局在効果に寄与も効いてくるものと考えられ、これらが電荷ドープ量に応じて競合した結果と解釈できる。
(BEDT-TTF = bis(ethylenedithio)tetrathiafulvalene)
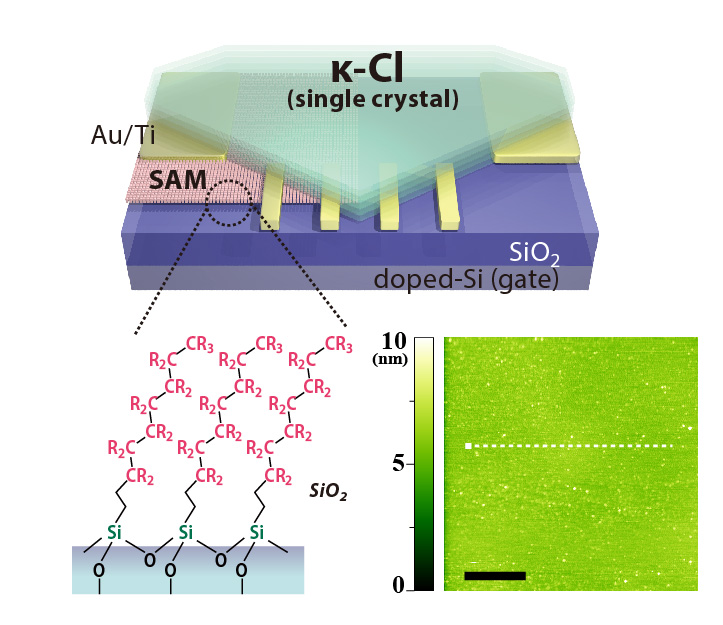
図1:SAM表面修飾絶縁基板を用いた有機モットFETの模式図(R = F, H)。
(右挿入図)κ-Cl単結晶表面の原子間力顕微鏡(AFM))。スケールバー:500 nm。
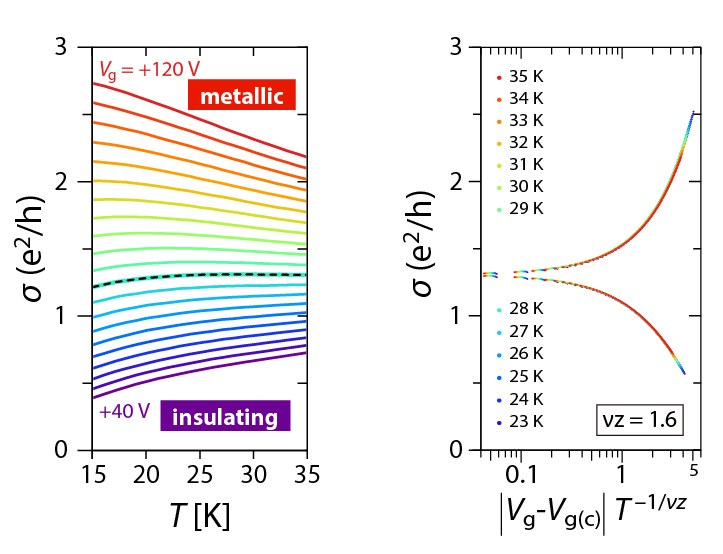
図2:SAM上κ-Clチャネルで観測された電界効果ドーピング誘起のMI転移。
(左)電気伝導度の温度変化におけるゲート電圧依存性。破線はMI転移境界線を示す。
(右)電気伝導度のスケーリングプロット。e2/h=38.7 μS。













