
Synthesis, characterization, and design of molecular materials, especially molecular conductors (including superconductors), have been undertaken. Molecular conductors exhibit a variety of physical properties which can be systematically understood on the basis of "simple" and "clear" electronic structures. From a chemical point of view, the most fascinating character of the molecular conductor is its "designability", that is, we can finely control solid state properties with chemical modifications of the molecule. The newly synthesized materials are characterized by the X-ray diffraction method and physical measurements (electrical conductivity...etc.). The electronic structure is investigated by the band structure calculation. All these results are devoted to the design of new molecular materials.
- Interplay between Spin, Charge, Lattice and Orbital in Molecule-Based Spin Liquid Revealed by Vibrational Spectroscopy (Kato; Yamamoto, Fujimoto, Naito Nakazawa, Tamura, Yakushi, Ikemoto, Moriwaki)
- Magnetic-Torque Study on Organic Triangular-Lattice Magnets, X[Pd(dmit)2]2, Located Near the Phase Boundary between Magnetic Order and Spin Liquid (Isono, Kato; Sugiura, Uji)
- Algebraic Charge Dynamics in Quantum Spin Liquid (Fujiyama, Kato)
- Nuclear Spin-Spin Relaxation of 13C in (Cation)[Pt(dmit)2]2 (Fujiyama, Kato)
- Pressure-Induced Metallic State of a Single-Component Molecular Crystal with a Trimer Structure, [Ni(ddt)2] (ddt = 1,4-dithiin-2,3-dithiolate) (Cui, Kato; Tsumuraya, Hamish, Chloe)
- Antiferromagnetic Insulating Phase of λ-(BETS)2FeCl4 Studied by Electron Spin Resonance (Oshima, Lee, Cui, Kato)
- Electron-Hole Symmetry in Molecular Massless Dirac Electron Systems (Kawasugi, Kato; Tajima, Suda, Yamamoto)
- Interplay between Spin, Charge, Lattice and Orbital in Molecule-Based Spin Liquid Revealed by Vibrational Spectroscopy
- Magnetic-Torque Study on Organic Triangular-Lattice Magnets, X[Pd(dmit)2]2, Located Near the Phase Boundary between Magnetic Order and Spin Liquid
- Algebraic Charge Dynamics in Quantum Spin Liquid
- Nuclear Spin-Spin Relaxation of 13C in (Cation)[Pt(dmit)2]2
- Pressure-Induced Metallic State of a Single-Component Molecular Crystal with a Trimer Structure, [Ni(ddt)2] (ddt = 1,4-dithiin-2,3-dithiolate)
- Antiferromagnetic Insulating Phase of λ-(BETS)2FeCl4 Studied by Electron Spin Resonance
- Electron-Hole Symmetry in Molecular Massless Dirac Electron Systems
Assign: Kato; Yamamoto, Fujimoto, Naito Nakazawa, Tamura, Yakushi, Ikemoto, Moriwaki
Molecule-based quantum spin liquids (QSLs) attract growing interest since any spin ordering is hindered below liquid helium temperature. In the crystal structures of β'-EtMe3Sb[Pd(dmit)2]2 (in Fig. 1), two-dimensional (= 2D) layers consisting of [Pd(dmit)2]2 dimer units belong to the triangular lattice. The recent studies revealed the following properties: 1) 2D layer is not always equilateral triangular lattice. 2) A subtle but non-negligible entropy release occurs near liquid helium temperature. These properties are not straightforwardly ascribed to the geometrical frustration in equilateral triangular lattice. We examined charge, lattice, and orbital frustrations in the QSL state by using the vibrational spectra of the C=C stretching modes. We observed the IR and Raman spectra in the QSL state of β'-EtMe3Sb[Pd(dmit)2]2 along with those in the antiferromagnetic states of β'-Me4P[Pd(dmit)2]2, β'-Et2Me2P[Pd(dmit)2]2 and β'-Me4Sb[Pd(dmit)2]2. The experimental results were compared with those in the non-magnetic and charge-ordered (NMCO) states associated with formation of tetramers or octamers.
Figure 2 shows the IR and Raman spectra in the QSL state of β'-EtMe3Sb[Pd(dmit)2]2 at 5 K. AIR and DIR belong to the C=C stretching modes of tetramers because similar modes are observed in the NMCO states of monoclinic-EtMe3P[Pd(dmit)2]2 and triclinic-EtMe3P[Pd(dmit)2]2. CO4 and the shoulder of DR belong to the C=C stretching modes of octamers because similar modes are observed in the NMCO states of β'-Et2Me2Sb[Pd(dmit)2]2 and β'-Cs[Pd(dmit)2]2. However, the intensities of four vibrational modes in the QSL state are significantly smaller than those in the NMCO states. The C=C stretching modes belonging to dimers (= BIR, CIR, AR, and DR) are also observed at 5 K. These results indicate that dimers, tetramers and octamers are frustrated in the QSL state (= lattice frustration). The linewidth of the charge sensitive mode (= BIR) is significantly larger than those in the AF states, which indicates inhomogeneous molecular charges. However, any peak separation characteristic of the NMCO states was not observed in BIR. These phenomena are ascribed to the charge frustration between dimers, tetramers and octamers.

Figure 1: Monomer of [Pd(dmit)2], crystal structure of β'-EtMe3Sb[Pd(dmit)2]2 viewed along the b axis, and two-dimensional triangular lattice consisting of tight dimer.

}QFFigure 2: IR-conductivity and Raman spectra in the QSL state of β'-EtMe3Sb[Pd(dmit)2]2 at 5 K.
Figure 3 shows the mechanism of the QSL state in β'-EtMe3Sb[Pd(dmit)2]2. Due to the strong dimerization, HOMOs and LUMOs in monomers constitute LUMO and HOMO in the dimer, respectively. In the NMCO states where tetramers or octamers are formed, the inter-molecular bond formation cooperates with charge separation. Not only magnetic order as a Mott insulator, but also tetramer and octamer become candidates for the ground state. The QSL state of β'-EtMe3Sb[Pd(dmit)2]2 is ascribed to the frustration between degenerated three states. Due to this mechanism, the QSL state survives even in the non-equilateral triangular lattice. The highest occupied energy levels of these states are lower than that of the isolated dimer. This degenerated states leads to an entropy release. Therefore, the interplay between spin, charge, lattice, and orbital plays a crucial role in the QSL state in β'-EtMe3Sb[Pd(dmit)2]2.

Figure 3: (top) Correlation diagram between energies in normal dimer, tight dimer, tetramer and octamer. (bottom) Schematic view of triangular lattice consisting of dimers, tetramers and octamers.
References
[1] T. Yamamoto, et. al., Sci. Rep., 7, 12930 (2017).
Assign: Isono, Kato; Sugiura, Uji
A quantum spin liquid (QSL) is an exotic novel ground state in magnetic materials, where electron spins continue to fluctuate even at zero temperature, because of strong quantum fluctuations. As is well known, conventional spin systems generally develop magnetic order such as ferromagnetic and antiferromagnetic (AF) states at low temperatures. However, these states are destabilized by a competing interaction (spin frustration), for instance, antiferromagnetically-coupled spins on a triangular lattice cannot satisfy the antiparallel paring on all bonds, as shown in the inset of Fig. 1a. Organic triangular-lattice antiferromagnets, X[Pd(dmit)2]2, were first synthesized in Kato Lab. A characteristic feature of these materials is that a degree of frustration (an anisotropy of a triangular lattice, t'/t) can be precisely controlled by chemical substitution of a cation X+. This feature allows us to study an exotic QSL state in a systematic phase diagram; as shown in Fig. 1a, as t'/t is increased, the AF state is gradually suppressed, and the QSL state appears in X = EtMe3Sb [1]. An important question here is how the AF order is disappeared. Possibly, the strong frustration effect may lead to a novel magnetic state between the AF and QSL states, or if the AF order is continuously suppressed to 0 K, critical phenomena may be observed near the quantum critical point.
Recently, we have performed torque magnetometry on AF materials, X = Me4P (TN ~ 40 K) and Me4Sb (TN ~ 15 K), and found that the uniaxial AF state is realized below the transition temperature, TN. In the present study, we have measured the magnetic torque on X = Et2Me2As0.75Sb0.25 and Et2Me2As0.65Sb0.35, in which the t'/t values are slightly larger than X = Et2Me2As. As the experiments for the two materials give the qualitatively same results, the results for X = Et2Me2As0.75Sb0.25 are shown below. Figure 1b depicts the field-angle dependence of the magnetic torque τ for X = Et2Me2As0.75Sb0.25. Here, a magnetic field is applied parallel to the crystallographic ac* plane. At T = 1.5 K, τ shows two-fold sinusoidal behavior even in the low-field region. This behavior is also observed in the relatively high-temperature region, where the amplitude of the sinusoidal curve is proportional to the square of magnetic field (Fig. 1d). The similar τ ε H2sin2θ behavior is observed for the bc* field rotation, as well. This behavior is a characteristic of conventional paramagnetic states (τ ~ ΔχH2sin2θ). For comparison, we present the torque curve at T = 1.5 K ( TN) for X = Me4Sb in Fig. 1c. Because of the spin-flop transition, τ exhibits complicated field-angle dependence in the low-field regime. The above results suggest that X = Et2Me2As0.75Sb0.25 is paramagnetic, and the uniaxial AF state is not realized down to T = 1.5 K. Torque magnetometry on X = Et2Me2As0.85Sb0.15, having the slightly smaller t'/t value than the present materials is needed in the future.
Figure 1d presents the temperature dependence of τ/H2 for X = Et2Me2As0.75Sb0.25. For bc* field rotation, τ/H2 is monotonically decreased with deceasing temperature, and becomes nearly temperature-independent below T ~ 5 K. This behavior is scaled to the static magnetic susceptibility χ, measured by Ueda et al. The deviation at low temperatures is attributed to impurity spins. On the other hand, for the ac* field rotation, τ/H2 shows nearly temperature-independent behavior from T = 50 K down to 1.5 K. In case of another organic spin-liquid candidate, κ-(BEDT-TTF)2Cu2(CN)3, the temperature dependence of τ/H2 is scaled to χ(T) for every field rotation, which allows us to discuss χ at very low temperatures, based on the torque data [2]. By contrast, in X = Et2Me2As0.75Sb0.25, τ/H2 is not simply scaled to χ. A possible explanation for this is that the temperature variation in the g factor along the principal axis, the stacking direction of Pd(dmit)2 columns, may be much different from that along the other principal axes.
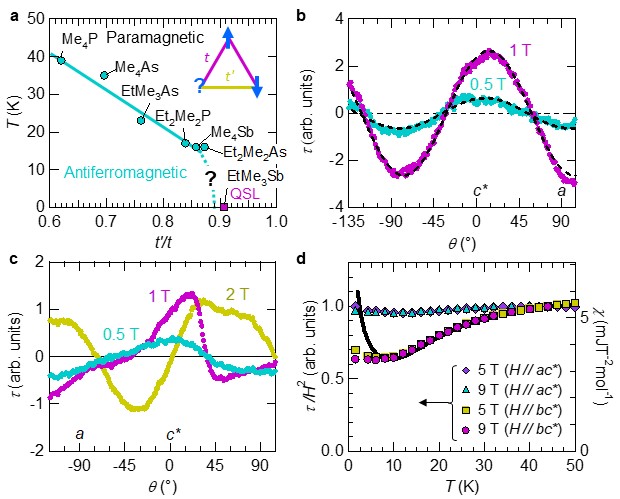
Figure 1: (a) Temperature-frustration (t'/t) phase diagram of X[Pd(dmit)2]2. (b) Field-angle dependence of the magnetic torque τ in low-field regions for X = Et2Me2As0.75Sb0.25. Dashed line represents a sinusoidal fitting curve, τ = Asin2(θ + θ0). (c) Field-angle dependence of the magnetic torque in low-field regions for X = Me4Sb. (d) Temperature dependence of the magnetic torque divided by the square of magnetic field, τ/H2, and the magnetic susceptibility, χ. Solid line represents the magnetic susceptibility measured by Ueda et al.
[1] R. Kato, Bull. Chem. Soc. Jpn., 87, 355 (2014).
[2] T. Isono et al., Nature Commun., 7, 13494 (2016).
Assign: Fujiyama, Kato
Quantum spin-liquids have attracted considerable attention in condensed matter physics. Geometrical frustration of the antiferromagnetic network in triangular or Kagome lattices is known to prevent classical Neel-type magnetic ordering with two sublattices and stabilize novel magnetic states. It was previously found that the ac responses of the dielectric constants of the molecular-based quantum spin liquids, β'-EtMe3Sb[Pd(dmit)2]2 and κ-(BEDT-TTF)2Cu2(CN)3, show similar anomalies[1]. However, the macroscopic dielectric constants cannot be compared with theoretical results, which limits quantitative understanding of the charge dynamics of QSL materials.
We measured the NMR for 1H, 2D, and 121Sb in the cation of β'-EtMe3Sb[Pd(dmit)2]2. The nuclear spin-lattice relaxation rates (1/ T1) and nuclear spin-spin relaxation rates (1/ T2) of the three elements have maxima caused by low-energy electronic fluctuations. We assign the temperature dependent correlation times with activation energies of ’= 2 ~ 102 and = 1.2 ~ 103 to the rotations of methyl (CH3) and ethyl (C2H5) groups by comparing 1/T1 of 1H and 2D for pristine and d9-deuterated [C2H5(CD3)3Sb] crystals. At the Sb site, on the other hand, we found unknown glassy slowing down of the charge fluctuation with a weakly temperature-dependent correlation time, which remains active down to the lowest temperatures [2].

Figure 1: Temperature dependent correlation times of the enhanced 1/T1 of H, D, and Sb in the cation of a quantum spin liquid, EtMe3Sb[Pd(dmit)2]2 and Me4Sb[Pd(dmit)2]2. Macroscopic characteristic time of the ac conductance is shown as a reference.
[1] M. A. Jawad, N. Tajima, R. Kato, and I. Terasaki., Phys. Rev. B, 88, 075139 (2013).
[2] S. Fujiyama and R. Kato, Phys. Rev. B, 97, 035131 (2018).
Assign: Fujiyama, Kato
Spin-orbit coupling in molecular solids has been recognized to offer minor effect on the electronic properties because molecules are composed of light elements.
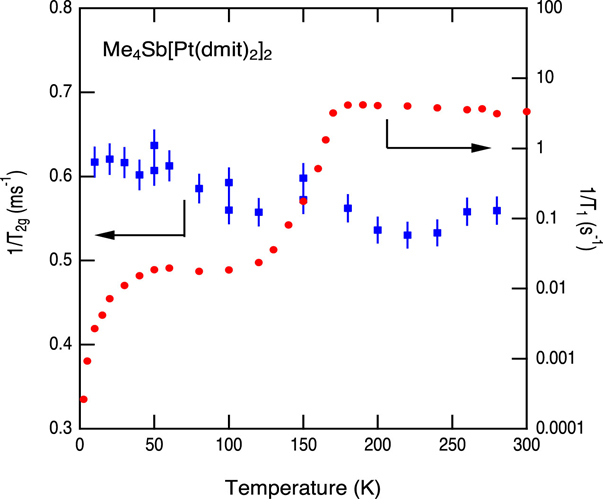
A metal complex (Cation)[Pt(dmit)2]2 containing 5d transition metal has an opportunity to study the effect of spin-orbit coupling in molecular solids. This material shows a metal-insulator transition at Tc = 160 - 200 K (depending on cations) associated with structural phase transition. Below Tc, the susceptibility becomes much smaller than that above Tc, and the electronic state has been considered as a band insulating state with a charge ordering. Below 50K, however, the 1/T1 shows strong temperature dependence. The 1/T1 is nearly proportional to temperature showing continuous spin excitation spectra following the Fermi-Dirac statistics.
We measured nuclear spin-spin relaxation rate 1/T2G of 13C of Me4Sb[Pt(dmit)2]2 to study the real part of the dynamical susceptibility at the lowest frequency with ~100 kHz. An assumption that quasi one-dimensional antiferromagnetic network is established below the phase transition temperature would expect the 1/T2G scaled with 1/T1. The obtained 1/T2G is nearly independent of temperature, which shows 1/T2G is dominated by direct dipolar interaction of nucleus. No scaling relation between 1/T2G and 1/T1 is found for the whole temperature range, and no positive indication of an establishing of quasi one-dimensional antiferromagnetic correlation. For T < 30K, where 1/T1 follows a Korringa relation, 1/T2G continues to enhance upon cooling. This result shows a gapless magnetic excitation in the ground state of this material.
References
[1] H. Fukuyama, J. Kishine, and M. Ogata, J. Phys. Soc. Jpn., 86, 13706 (2017).
Assign: Cui, Kato; Tsumuraya, Hamish, Chloe
In the development of single-component molecular conductors, metal dithiolene complexes, with a small energy gap between HOMO and LUMO, have formed an important category [1,2]. On the other hand, molecular crystals have a soft lattice, and thus an application of pressure to insulating single-component molecular crystals is very efficient way to discover new single-component molecular metals or superconductors. Indeed, we have modified the four-probe resistivity measurement technique by using a Diamond Anvil Cell (DAC), and successfully found that insulating [Ni(ptdt)2] (ptdt = propylenedithiotetrathiafulvalenedithiolate) [3], [Cu(dmdt)2] (dmdt = dimethyltetrathiafulvalenedithiolate) [4], and [Ni(dmit)2] (dmit = 1,3-dithiole-2-thione-4,5-dithiolate) [5] turned metallic at 19.4 GPa, 4.7 GPa, and 15.9 GPa, respectively. Recently, we also found the first single-component molecular superconductor based on metal dithiolene complex [Ni(hfdt)2] (hfdt = bis(trifluoromethyl)tetrathiafulvalenedithiolate) at 8 GPa (Tc= 5.5 K) [6]. We have employed density functional theory (DFT) calculations for single-component molecular crystal [Pd(dddt)2] (dddt=5,6-dihydro-1,4-dithiin-2,3- dithiolate) that exhibits temperature independent resistivity at 12.6 GPa. The result indicates that Dirac cones emerge in [Pd(dddt)2] under high pressure. [7]. Here, we report the crystal structure and the pressure dependent resistivity of [Ni(ddt)2] (ddt = 1,4-dithiin-2,3-dithiolate: Fig. 1a) with trimer-based structure.

Figure 1: Molecular and crystals structure of trimer structure [Ni(ddt)].
Figure 2 shows the temperature dependence of resistivity under pressure for [Ni(ddt)2] with the trimer-based structure. The system was semiconducting at ambient pressure, the room temperature conductivity (δrt) and activation energy (Ea) were 7 x 10-3 S cm-1 and 58 meV, respectively. With increasing pressure, the room temperature resistivity and Ea rapidly decreased. At 8.9 GPa, rt increased by four orders of magnitude (11 S cm-1) and the temperature dependence of resistivity was still semiconducting with very small Ea (0.4 meV). The metallic behavior appeared at 11 GPa, and the system remained metallic down to ~ 25 K, then a small upturn of the resistivity was observed. At the lowest temperature (3.9 K), the resistivity was only twice as high as the room temperature value. Above 11 GPa, however, the system turned semiconducting again, and both resistivity and Ea increased with increasing pressure (Figure 3) To understand the electronic state under high pressure, the first-principles DFT calculations were performed. The single crystal structure analysis under high pressure was also performed using synchrotron radiation. Both results show good agreement with resistivity measurement results.

Figure 2: Temperature and pressure (< 11.0 GPa) dependences of the resistivity of [Ni(ddt)2] with the trimer-based structure.
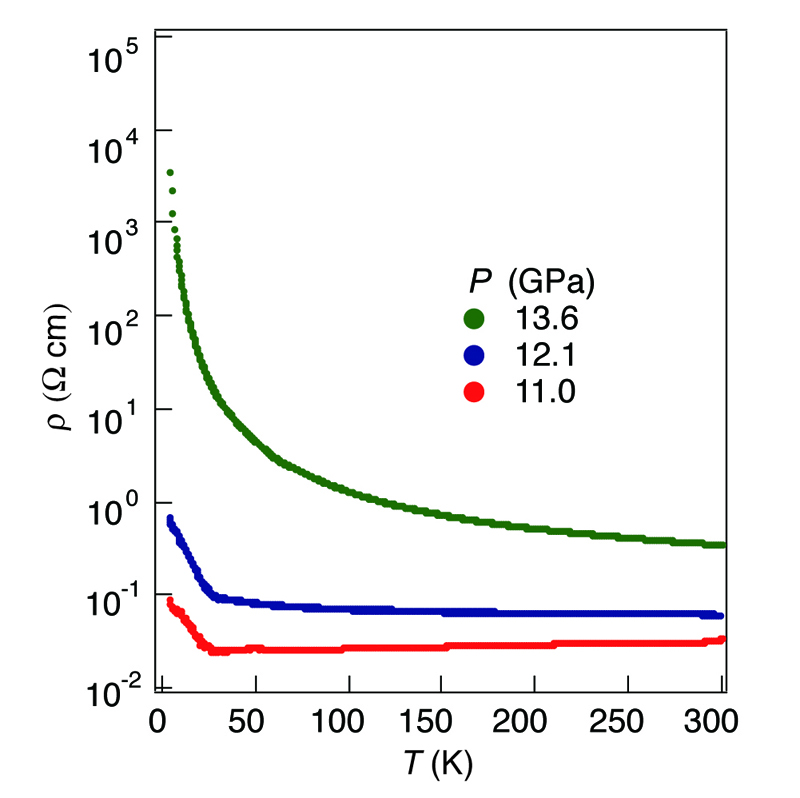
Figure 3: Temperature and pressure (>11.0 GPa) dependences of the resistivity of [Ni(ddt)2] with the trimer-based structure.
References
[1] H. Tanaka et al., Science, 291, 285 (2001).
[2] W. Suzuki et al., J. Am. Chem. Soc., 125, 1486 (2003).
[3] H. B. Cui et al., J. Am. Chem. Soc., 131, 6358 (2009).
[4] B. Zhou et al., J. Am. Chem. Soc, 134, 12724 (2012).
[5] H. B. Cui et al., Eur. J. Inorg. Chem., 24, 3837 (2014).
[6] H. B. Cui et al., J. Am. Chem. Soc., 136, 7619 (2014).
[7] R. Kato et al., J. Am. Chem. Soc., 139, 1770 (2017).
[8] H. Kim et al., Bull. Chem. Soc. Jpn., 61, 2559 (1988).
Assign: Oshima, Lee, Cui, Kato
Molecular conductors with finite π-d interaction have attracted considerable interests for the past few decades since the interaction between the itinerant π-electron and localized d-electron yields some intriguing physical phenomena. A molecular conductor λ-(BETS)2FeCl4 is one of the such materials which shows interesting physical properties. Although it is well known that this salt shows superconducting state above 17 T when the magnetic field is applied along the conducting plane, [1] the ground state at low temperature is also interesting. Although its high-temperature phase is paramagnetic and metallic (hereafter, PM phase), this salt shows a metal-insulator (MI) transition, and becomes simultaneously antiferromagnetic at TMI=8.3 K known as the antiferromagnetic insulating (AFI) phase. The origin of the antiferromagnetic state, whether the d-electrons or the π-electrons trigger the antiferromagnetic state, has been discussed for a long time. However, recent specific heat measurements revealed that the broad excess specific heat observed below TMI can be fit with the Schottky peak in which the energy level of Fe3+ (S=5/2) is split into six levels by an internal field of 4 T. Therefore, it is now considered that only π-electrons become antiferromagnetic (inducing an internal field of 4 T), and the d-electrons of Fe3+ remain paramagnetic. [2] However, previous ESR studies did not observe electron paramagnetic resonance (EPR) in the AFI phase, and only antiferromagnetic resonance (AFMR) was reported. [3-5] To resolve these issues, we are performing ESR measurements with λ-(BETS)2FeCl4, and studying its angular and temperature dependences in detail.
Last fiscal year, we studied EPR of λ-(BETS)2FeCl4 in the PM phase, and reported that the angular dependence has some characteristic feature owing to the strong π-d interaction. Moreover, we proposed a method to find the antiferromagnetic easy-axis from the angular dependence of EPR. This fiscal year, we applied the magnetic field along the easy-axis by using this method, and studied the AFMR in detail.
Figure 1 shows the temperature dependence of ESR spectra for B//easy-axis. Two absorption lines were observed for this direction. While the ESR absorption line observed at higher magnetic field is temperature independent, the absorption line for lower magnetic field shifts as the temperature increases, then, merges with the EPR line around TMI. The resonance field for the higher ESR absorption line is observed around 1150 mT, which corresponds to the spin-flop field observed in magnetic torque measurements [6]. Hence, from its characteristic behavior, the higher and lower ESR absorption lines are attributed to the spin-flop resonance and easy-axis mode of AFMR, respectively. It is noteworthy that the spin-flop resonance is observed up to 11 K, which is higher than the MI transition temperature, TMI=8.3 K. Although the antiferromagnetic long-range order and the MI transition are considered to occur simultaneously, our result suggests that the magnetic transition occurs above TMI in the PM phase. Note that the spin-flop resonance above TMI is very small, hence, it is considered that the antiferromagnetic state above TMI is only partial.
Since AFMR was observed in the PM phase, we verified whether EPR can be observed in the AFI phase or not. The integrated intensities of AFMR and EPR are presented in Fig. 2. The magnetic field is applied parallel to the easy-axis and the integrated intensity of AFMR was taken from the spin-flop resonance. AFMR was observed below 11 K, and its intensity gradually increased with decreasing temperature. On the other hand, EPR's integrated intensity showed a Curie-like behavior in the high temperature region, and started to decrease below 12 K. Below TMI, EPR absorption line was still observed and vanished below 6 K. This suggests that the paramagnetic and antiferromagnetic states coexist at the boundary between the PM and AFI phases. Such coexistence of two magnetic states around TMI was also reported from the Mossbauer measurement [7].
It was considered that the antiferromagnetic long-range order of λ-(BETS)2FeCl4 is a first order transition. However, our results suggest a second-order like transition where a slow transition from paramagnetic to antiferromagnetic state is observed. Moreover, the integrated intensity of AFMR only showed a gradual increase with decreasing temperature, and no drastic change was observed around TMI. This result is quite surprising since there is a clear divergence of the specific heat at TMI, and this discrepancy needs to be explained. We are planning to study the sample dependence and the cooling dependence of the integrated intensity.

Figure 1 (Left): Temperature dependence of AFMR spectra.
Figure 2 (Right): Temperature dependence of AFMR and EPR integrated intensity.
References
[1] S. Uji et al., Nature, 410, 908 (2001).
[2] H. Akiba et al., J. Phys. Soc. Jpn., 78, 033601 (2009).
[3] L. Brossard et al., Eur. Phys. B, 1, 439 (1998).
[4] T. Suzuki et al., Phys. Rev. B, 67, 020408(R) (2003).
[5] I. Rutel et al., Phys. Rev. B, 68, 144435 (2003).
[6] T. Sakaki et al., Synth. Met., 120, 759 (2001).
[7] J. C. Waerenborgh et al. Phys. Rev. B, 81, 060413 (2010).
Assign: Kawasugi, Kato; Tajima, Suda, Yamamoto
Since the discovery of graphene, condensed matter physics based on massless Dirac particles has attracted considerable attention. Linear energy dispersion structures have led to such the novel phenomena as the half integer quantum Hall effect and the Klein tunneling effect. Recently, a number of materials with massless Dirac particles have been discovered, resulting in the rapid development of the physics of Dirac fermion systems. Among them, we have discovered the massless Dirac electron system next to the charge ordered insulating phase in the temperature-pressure phase diagram of an organic conductor α-(BEDT-TTF)2I3. Thus, this system provides a testing ground for the investigation of physical phenomena in strongly correlated Dirac particles. According to Elias, the Dirac cones were reshaped by the effects of the Coulomb interaction [1]. The reshaped Dirac cones by the Coulomb interaction were reexamined in α-(BEDT-TTF)2I3 under the high pressure approximately 2.3 GPa by Hirata [2].
Is the electron-hole symmetry of the strongly correlated Dirac electron system maintained? To address this question, thin crystals which holes or electrons were injected by the contact electrification were prepared so that the quantum transport phenomena were investigated [3]. The Fermi velocities vFe and vFh of upper and lower Dirac cones were examined from the detection of the Shubnikov-de Haas oscillations. The ratio vFe/vFh is estimated to be approximately 1.3. This is the electron-hole symmetry of this system.

Figure 1: Dirac cone symmetry in α-(BEDT-TTF)2I3
[1] D. C. Elias et al., Nature Phys., 7, 701(2011).
[2] M. Hirata et al., Nature Comm., 7, 12666 (2016).
[3] N. Tajima et al., Phys. Rev. B, 88, 075315 (2013).












